Geometric Progression Sum to Infinity
So our infnite geometric series has a finite sum when the ratio is less than 1 and greater than 1 Lets bring back our previous example. This file is prepared by the best academic experts in India.

Mathwords Infinite Geometric Series
For example if there is a quadratic polynomial.

. In geometric progressions where r 1 in other words where r is less than 1 and greater than 1 the sum of the sequence as n tends to infinity approaches a value. So what happens when n goes to infinity. The formula works for any real numbers a and r except.
Letting a be the first term here 2 n be the number of terms here 4 and r be the constant that each term is multiplied by to get the next term here 5 the sum is given by. It is very useful while calculating the Geometric mean of the entire. Now learn how t o add GP if there are n number of terms present in it.
Where b 1 - is the first element of the geometric series in our case it. Close Log In. .
In other words if you keep adding together the terms of the sequence forever you will get a finite value. In Maths NCERT Solutions Class 10 Chapter 5 students will learn about the arithmetic progression. And r should not be 0 because the sequence a00 is not geometric.
In an arithmetic sequence and series a is represented as the first term d is a common difference a n as the nth term and n as the number of terms. In general the arithmetic sequence can be represented as a ad a2d a3d. Remember me on this computer.
In the example above this gives. The following points are helpful to clearly understand the concepts of sequence and series. R must be between but not including 1 and 1.
Where r is a constant which is known as common ratio and none of the terms in the sequence is zero. If r 1 r 1 r 1 then the sum to infinity is given by. Students can download this PDF file by visiting Vedantu.
Every answer is written according to the. Arithmetic Progression Geometric Progression Video 0256 min. Arithmetic Progression Sum of Nth terms of GP.
4 4 4 4 B. What all will you get under EduRev Infinity Package for CAT. Geometric series ua n r n-1 S r ar r 1 1 n 1 n --S r a r 1 1 1 3-2.
An arithmetic-geometric progression AGP is a progression in which each term can be represented as the product of the terms of an arithmetic progressions AP and a geometric progressions GP. Arithmetic Mean Sum of all terms in the AP Number of terms in the AP. Log in with Facebook Log in with Google.
The arithmetic and geometric progression Maija Liepa. Doc 6 pages. Grade 10 Science Module 1st Quarter Luwen.
For Infinite Geometric Series. Once you start diving into the topic of what is an arithmetic sequence its likely that youll encounter some confusionIt happens because of various naming conventions that are in use. Log In Sign Up.
It is known that the sum of the first n elements of geometric progression can be calculated by the formula. N will tend to Infinity n Putting this in the generalized formula. S n b 1 q n 1 q 1.
We can use this formula. A n ar n-1. A geometric series is a sum of an infinite number of terms such that the ratio between successive terms is constant.
Sum to Infinite GP - Algebra Quantitative Reasoning Video. For example the series is geometric because each successive term can be obtained by multiplying the previous term by In general a geometric series is written as where is the coefficient of each term and is the. Product of the Geometric series.
The NCERT Solutions for Class 10 Maths Chapter 5 PDF file available for free can help students to score good marks. The Product of all the numbers present in the geometric progression gives us the overall product. Sum of n terms of an AP 05 n first term last term 05 n 2a n-1 d Geometric Progression GP A sequence of numbers is called a geometric progression if the ratio of any two consecutive terms is always same.
Geometric series Jhon Paul Lagumbay. 120 days study plan to prepare for CAT with EduRev Doc. It is basically the addition of squared numbers.
Click here to sign up. Find the sum to infinity of each geometric sequence if it exists. A geometric progression has third term of 8 and sixth term of 0064.
A geometric series is the sum of the numbers in a geometric progression. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. Therefore to calculate series sum one needs somehow to find the expression of the partial series sum S nIn our case the series is the decreasing geometric progression with ratio 13.
Enter the email address you signed up with and well email you a reset link. Vietas formula relates the coefficients of polynomials to the sums and products of their roots as well as the products of the roots taken in groups. Sequence and Series Tips.
N th term for the GP. Two of the most common terms you might encounter are arithmetic sequence and seriesThe first one is also often called an arithmetic progression while the second one is also named. O Level Additional Mathematics 403724 Paper 2 MayJun 2021.
The sum to infinity of a geometric progression. Sum of squares refers to the sum of the squares of numbers. Find the sum to infinity of this progression.
The squared terms could be 2 terms 3 terms or n number of terms first n even terms or odd terms set of natural numbers or consecutive numbers etc. This value is equal to. 8 terms of 3 3 3 3.

Geometric Series Sum To Infinity Examsolutions Youtube

Proof Of The Geometric Series Formula Finite Infinite Youtube
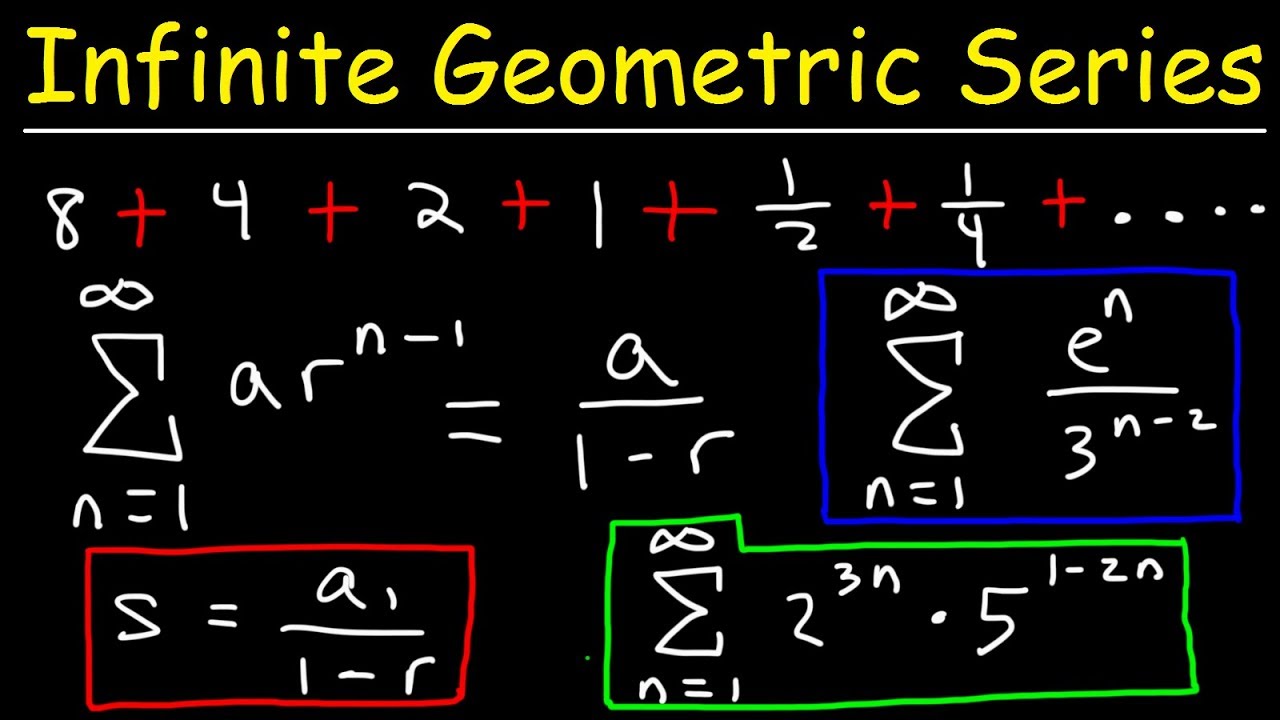
Finding The Sum Of An Infinite Geometric Series Youtube
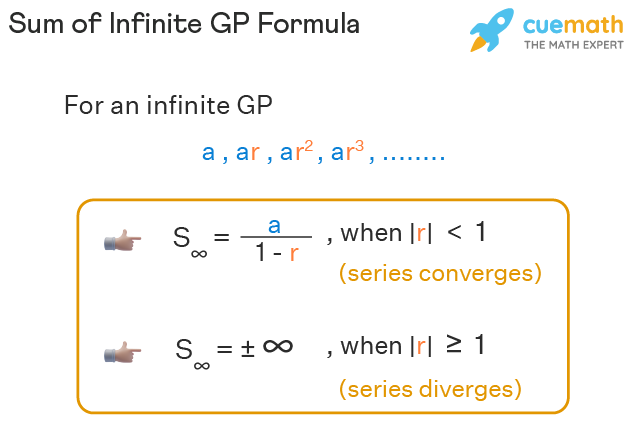
Sum Of Infinite Gp Formula Sum Of Infinite Terms Of Gp
0 Response to "Geometric Progression Sum to Infinity"
Post a Comment